Conjugado

O conjugado de um número complexo desempenha função importante nas operações dentro desse conjunto.

O Conjunto dos números complexos (C) é formado pelos pares ordenados de números reais, Z= x + yi, se somente se x R e y R. Z C. Todo número complexo Z= (x, y) pode ser escrito na forma:

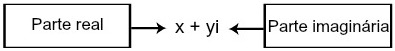
Exemplos: 2 +3i, 1+ i, 3i, 5i, 2-3i

Seja um número complexo: , seu conjugado será 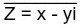, para obtê-lo apenas trocamos o sinal da parte imaginária do número, ou seja, a parte real permanece igual e as imaginárias são simétricas.

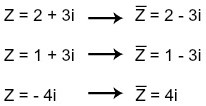
Exemplos:

Operações com conjugado

Observe que se multiplicarmos um número complexo por seu conjugado obteremos um número real.

(1+ 2i). (1- 2i)

1 - 2i + 2i - (2i)²

1² – (2i)²

1+ 4= 5 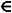R. * i² = - 1

Consideremos os números Z₁= 3 + i e Z₂ = 2 + i, façamos a divisão de Z₁ por Z₂:

3 + i
2 + i

Não pare agora... Tem mais depois da publicidade ;)

3 + i • 2 - i
2 + i 2 - i

6 – 3i + 2i – i²
2² - i ²

7 - i
4 - (-1)

7 - 1 i
5 5

O conjugado é utilizado para efetuar a divisão entre números complexos, note que multiplicamos o numerador e o denominador pelo conjugado do denominador.

Com tudo, podemos estabelecer as propriedades do conjugado de um número complexo:

|Z| = |Z| O módulo do conjugado de um número complexo será o mesmo módulo do número;

Z . Z = |Z|² O produto de um número complexo pelo seu conjugado é o quadrado do módulo desse número, portanto, um número Real;

Z + Z = 2 x 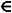R A soma de um número complexo ao seu conjugado resulta no dobro da parte real do número;

Z – Z= 2yi 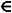C A subtração de um número complexo com seu conjugado resulta no dobro da parte imaginária desse número.

Publicado por Camila Garcia