Propriedades das Proporções
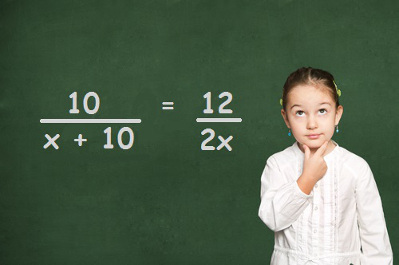
A razão entre dois números é dada pela divisão desses números, por exemplo, a razão entre a e b é dada por a/b. Quando estabelecemos uma relação de igualdade entre duas razões, temos uma proporção. Suponha a seguinte proporção:
a = c
b d
Essa proporção pode ser expressa da seguinte forma:
a : b = c : d
Os itens em vermelho são classificados como extremos e os itens em azul são os meios.
Temos então a Propriedade Fundamental das Proporções, que nos garante que “o produto dos extremos é igual ao produto dos meios”. Essa propriedade é comumente chamada de multiplicação cruzada. Vejamos:
a = c
b d
a.d = b.c
Mas além dessa, temos outras propriedades que podem nos ajudar muito a resolver problemas com proporções, são elas:
a) Trocar os extremos
a = c ←→ d = c
b d b a
a.d = b.c ←→ d.a = b.c
b) Trocar os meios
a = c ←→ a = b
b d c d
a.d = b.c ←→ a.d = c.b
c) Inverter as duas razões
a = c ←→ c = d
b d a b
a.d = b.c ←→ c.b = a.d
d) Trocar a posição das duas razões
a = c ←→ c = a
b d d b
a.d = b.c ←→ c.b = d.a
A partir dessas propriedades das proporções, chegamos a duas importantes relações entre razões:
a = c ←→ a + c = a ou a + c = c
b d d + b b d + b b
a = c ←→ a – c = a ou a – c = c
b d d – b b d – b b
Exemplos:
1. Se x = y e x + y = 15, calcule o valor de x e de y.
4 6
a = c ←→ a + c = a
b d d + b b
Temos a seguinte proporção
x = y
4 6
Aplicando a propriedade destacada, temos:
x + y = x
6 + 4 4
Mas nós temos a informação de que x + y = 15, substituindo x + y na proporção anterior, temos:
15 = x
10 4
Aplicando a Propriedade Fundamental das Proporções, temos que o produto dos extremos é igual ao produto dos meios, portanto:
15.4 = x.10
x.10 = 15.4
x.10 = 60
x = 60
10
x = 6
2. Vamos resolver a proporção da imagem inicial do texto? Para resolvê-la, aplicaremos a Propriedade Fundamental das Proporções.
10 = 12
x + 10 2x
10 . 2x = 12. ( x + 10 )
20x = 12x + 120
20x – 12x = 120
8x = 120
x = 120
8
x = 15
Artigos Relacionados

Últimas notícias
Outras matérias


















