Números pares e ímpares

Números pares e ímpares são as duas classificações dos números. O número é classificado como par se ele é divisível por 2, ou seja, deixa resto 0 na divisão por 2. O número é ímpar caso ele não seja divisível por 2, logo o resto da divisão desse número por 2 é igual a 1. Para certificar-se de que um número é par ou ímpar, basta analisar o algarismo da unidade desse número. Se a unidade for 0, 2, 4, 6 ou 8, o número é par; caso seja 1, 3, 5, 7 ou 9, o número é ímpar.

Leia também: Números triangulares — os números que podem ser representados na forma de triângulos

O que são números pares?

O número é classificado como par se ele for um número divisível por 2. Isso significa que esse número deixa resto 0 na divisão por 2. Dado um conjunto de objetos, se há uma quantidade par de objetos, significa que podemos dividir esse grupo ao meio, em duas partes iguais.

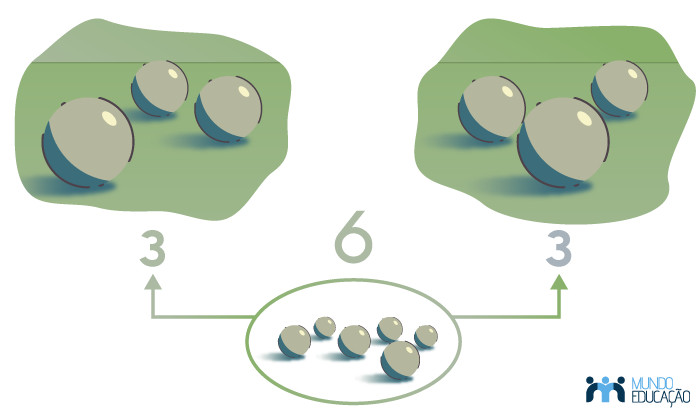
Para analisar se um número é par, basta verificar se o algarismo que ocupa a casa das unidades desse número é um número par também. Sendo assim, os números que possuem na casa da unidade um entre os números 0, 2, 4, 6 ou 8 são números pares.

Exemplos de números pares:

• 1024 → é par, pois a sua unidade é 4.

• 2130 → é par, pois a sua unidade é 0.

• 13572→ é par, pois a sua unidade é 2.

O que são números ímpares?

O número é classificado como ímpar se ele não é divisível por 2. Isso significa que esse número deixa resto 1 na divisão por 2. Dado um conjunto de objetos, se há uma quantidade ímpar de objetos, significa que não é possível dividir esse grupo ao meio, em duas partes iguais, pois sempre restará um objeto.

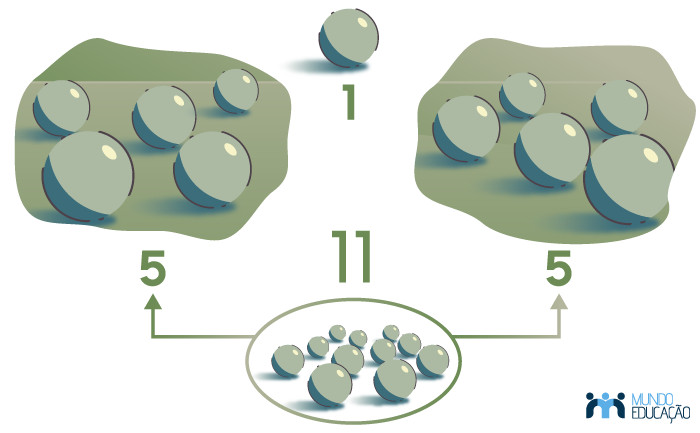
Para analisar se um número é ímpar, verificarmos se o algarismo que ocupa a casa das unidades é um número ímpar também, pois os números que possuem na casa das unidades um entre os números 1, 3, 5, 7 ou 9 são números ímpares.

Exemplos de números ímpares:

• 2049 → é ímpar, pois a sua unidade é 9.

• 3221 → é ímpar, pois a sua unidade é 1.

• 24685→ é ímpar, pois a sua unidade é 5.

Propriedades dos números pares e ímpares

• Propriedade 1: A soma de dois números pares é sempre um número par.

Seja 2n um número par e 2m outro número par, de modo geral, temos que:

\(2n+2m=2(m+n)\)

Como o resultado é um número múltiplo de 2, então ele também é um número par.

• Propriedade 2: A soma de dois números ímpares é sempre um número par.

Seja 2n + 1 e 2m + 1 dois números ímpares, temos que:

\(2n+1+2m+1=2n+2m+2\)

\(2n+1+2m+1=2(n+m+1)\)

Note que o resultado é um número múltiplo de 2, logo ele é um número par.

• Propriedade 3: O produto entre dois números pares é um número par.

Seja 2n e 2m dois números pares, temos que:

\(2n⋅2m=4mn\)

Sabemos que o resultado é um número múltiplo de 4, logo o resultado é um número par.

• Propriedade 4: O produto entre dois números ímpares é um número ímpar.

Seja 2n + 1 e 2m + 1 dois números ímpares, temos que:

\((2n+1)(2m+1)=4mn+2n+2m+1\)

\(2(n+1)(2m+1)=2(n+m+2mn)+1\)

Note então que esse número não é múltiplo de 1, portanto ele é um número ímpar.

Veja também: Números primos — os números que são divisíveis apenas por um e por eles mesmos

Exercícios resolvidos sobre números pares e ímpares

Questão 1

A soma dos 5 primeiros números pares maiores que 10 é igual a:

A) 65

B) 70

C) 75

D) 80

E) 85

Resolução:

Alternativa D

Os primeiros números pares maiores que 10 são 12, 14, 16, 18 e 20. Somando-os, obtemos:

\(12+14+16+18+20=80\)

Questão 2

Analise as afirmativas a seguir:

I. A soma entre dois números ímpares é um número ímpar.

II. A subtração de a – b, com a > b e a,b ímpar, é um número par.

III. O produto entre dois números pares é um número par.

Marque a alternativa correta:

A) Somente a afirmativa I é falsa.

B) Somente a afirmativa II é falsa.

C) Somente a afirmativa III é falsa.

D) Todas as afirmativas são verdadeiras.

Resolução:

Alternativa A

I. A soma entre dois números ímpares é um número ímpar. (Falso)

Seja 2n + 1 e 2m + 1 dois números ímpares, a soma desses números é igual a:

2n + 1 + 2m + 1 = 2n + 2m + 2 = 2(n + m + 1)

Note que esse número é múltiplo de 2, logo ele é um número par.

II. A subtração de a – b, com a > b e a,b ímpar, é um número par. (Verdadeiro)

Seja a = 2n + 1 e b = 2m + 1, temos que:

\(2n+1-(2m+1)=2n+1-2m=1=2n-2m=2(n-m)\)

O resultado é múltiplo de 2, logo ele é par.

III. O produto entre dois números pares é um número par. (Verdadeiro)

Seja 2n e 2m dois números pares, temos que:

\(2n⋅2m=4nm \)

Como 4 é múltiplo de 2, o produto é um número par.