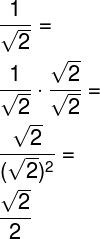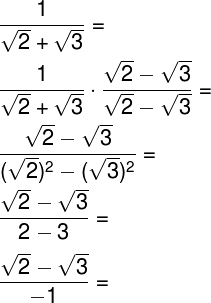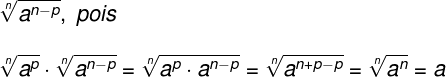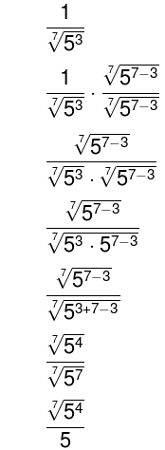Racionalização com raízes enésimas

Após simplificar expressões algébricas ou numéricas, é possível que o resultado possua um radical no denominador. Sabendo que uma raiz não exata é sempre um número irracional, uma divisão na qual o denominador contenha um número desses pode ser muito complicada. O processo de racionalização foi criado para simplificar esses cálculos, encontrando uma fração equivalente que não tem radical no denominador.
Os casos de racionalização são os seguintes:
1 – Fração com uma raiz quadrada no denominador
Suponha que a fração A possua numerador “a” e denominador “b”, em que “b” seja uma raiz quadrada. Para racionalizar a fração A, basta multiplicá-la pela fração:
b
b
Depois, deve-se simplificar o resultado obtido. Veja um exemplo de racionalização a seguir:
2 – Denominador com uma soma ou diferença
Caso o denominador de uma fração A contenha uma soma ou diferença envolvendo uma ou duas raízes quadradas distintas, devemos multiplicar essa fração por outra fração, em que numerador e denominador devem ser iguais ao conjugado do denominador da fração A.
A soma a + b tem conjugado igual a a – b. Exemplo:
3 – Denominador com uma raiz enésima
Seja n o índice de uma raiz, na qual o radicando é ap, considere a fração A, cujo denominador é essa raiz. O radical pelo qual multiplicaremos numerador e denominador da fração A será:
Observe, por exemplo, a racionalização da fração a seguir:
Artigos Relacionados

Últimas notícias
Outras matérias