Critérios de divisibilidade
Critérios de divisibilidade são ferramentas utilizadas a fim de facilitar os problemas que envolvem a divisão, já que, quando vamos realizar essa operação, temos duas opções em relação ao resultado, ou a resposta é exata ou não.
Quando a resposta é exata, dizemos que os números são divisíveis e o resto da divisão é zero. Agora, quando a divisão não é exata, dizemos que os números não são divisíveis e o resto da divisão é diferente de zero. Assim, para evitar a realização de uma imensidade de contas de divisão, estabeleceremos alguns critérios de divisibilidade dos números (de 1 a 10).

Veja mais: Propriedade fundamental das proporções
Divisibilidade por 1
O critério de divisibilidade por 1 é o mais trivial, visto que todo número inteiro é divisível por 1. Veja:
Seja A um número inteiro, assim:
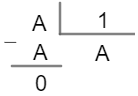
Acabamos de mostrar que, para qualquer que seja seu valor, A sempre será divisível por 1.
Divisibilidade por 2
Um número inteiro é divisível por 2 caso ele seja par, ou seja, todos os números cujo último algarismo é 0, 2, 4, 6 ou 8.
-
Exemplos
1020 é divisível por 2?
Sim, pois o último algarismo é 0, ou seja, podemos dizer que a divisão entre 1020 por 2 é exata. Seguindo o algoritmo da divisão, veja:
1020 = 510 ·2 + 0
Observe que o resto é 0, assim o número é divisível por 2.
1.000.006 é divisível por 2?
Note que o número em questão é relativamente grande, mas tem como último algarismo o número 6, que é par, assim o número 1.000.006 é divisível por 2.
53 é divisível por 2?
O número 53 não é divisível por 2, pois não tem como último algarismo um número par. Veja:
53 = 26 ·2 + 1
Divisibilidade por 3
Diremos que um número é divisível por 3 quando a soma dos seus algarismos é divisível por 3. Veja o exemplo:
324 é divisível por 3, pois 3 + 2 + 4 = 9. Como a soma é divisível por 3, o número 324 é divisível. Veja:
324 = 108 · 3 + 0
Divisibilidade por 4
Um número vai ser divisível por 4 quando os dois últimos algarismos também são divisíveis por 4, além disso, os números terminados em 00 também são divisíveis por 4.
-
Exemplos
O número 1500 é divisível por 4, pois termina em 00.
1500 = 375 · 4 + 0
1724 também é divisível por 4, pois seus dois últimos algarismos são divisíveis por 4.
1524 = 381 ·4 + 0
Divisibilidade por 5
Todos os números que possuem como último algarismo os números 0 ou 5 são divisíveis por 5.
-
Exemplos
O número 50 é divisível por 5, pois seu último algarismo é 0.
O número 1.000.525 é divisível por 5, visto que seu último algarismo é 5.
Leia mais: Divisão inversamente proporcional
Divisibilidade por 6
Todos os números que são divisíveis por 2 e por 3 ao mesmo tempo são divisíveis por 6.
-
Exemplos
O número 66 é divisível por 2 e 3, assim, o número 66 é divisível por 6. Veja:
66 = 6 · 11 + 0
2154 também é divisível por 2 e 3, logo, é divisível por 6.
Divisibilidade por 7
O critério de divisibilidade por 7 é o que exige mais atenção. Devemos duplicar o algarismo das unidades e subtrair o resto do número. Se o resultado dessa operação for divisível por 7, então o número é divisível por 7.
Pegue o número 1057, considerando seus dois últimos algarismos e multiplicando-os por 2, temos:
7·2 = 14
Agora pegando o resto do número, temos:
105 – 14 = 91
O número 91 é divisível por 7, pois 91 = 13 · 7 + 0. Logo, o número 1057 é divisível por 7, visto que 1057 = 151 · 7 + 0.
Divisibilidade por 8
Todo número terminado em 000 ou se os três últimos algarismos forem divisíveis por 8, então esse número será divisível por 8.
-
Exemplos
7000 é divisível por 8, visto que o número termina em três zeros. Assim temos:
7000 = 875 · 8 + 0
O número 29.584 também é divisível por 8, pois os três últimos algarismos são divisíveis por 8.
584 = 73 · 8 + 0
Assim, 29.584 é divisível por 8.
Divisibilidade por 9
Se a soma de todos os algarismos de um certo número é divisível por 9, então esse número é divisível por 9. Veja o exemplo:
O número 6.282 é divisível por 9, pois 6 + 2 + 8 + 2 = 18. Como 18 é divisível por 9, então o número 6.282 é divisível por 9.
Divisibilidade por 10
Todos os números terminados em 0 são divisíveis por 10.
Os números 10, 100, 1000, ..., e todos os seus múltiplos são divisíveis por 10.
-
Exemplos
3230 é divisível por 10, pois o número termina em 0.
3230 = 323 · 10 + 0
Não é necessário estabelecer mais critérios de divisibilidade, visto que todos os números enquadram-se nos critérios aqui destacados.
Artigos Relacionados

Últimas notícias
Outras matérias


















