Relações métricas no hexágono regular inscrito
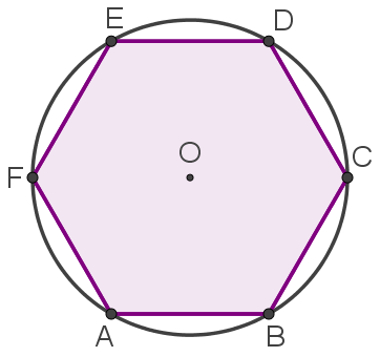
Dizemos que um polígono está inscrito quando existe uma circunferência que contém todos os seus vértices. Além disso, um polígono é regular quando ele possui todos os lados com a mesma medida e seus ângulos internos são congruentes. Portanto, um hexágono regular inscrito é um polígono que possui seis lados com a mesma medida e seis ângulos internos congruentes e cujos vértices são todos pontos pertencentes a uma circunferência. Veja na figura abaixo um hexágono regular inscrito:
As relações métricas no hexágono regular inscrito são fórmulas que podem ser usadas para encontrar a medida de seu lado e a medida de seu apótema a partir apenas do raio da circunferência na qual ele está inscrito. Essas fórmulas são:
l = r
Em que o raio da circunferência é igual ao lado do hexágono e:
a = r√3
2
Nessa fórmula, a é o apótema e r é o raio da circunferência.
Construções e elementos no hexágono inscrito
Antes de discutir essas fórmulas, convém realizar algumas construções no hexágono a fim de que suas demonstrações tornem-se mais diretas.
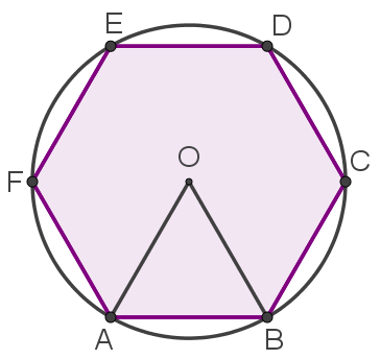
1º – Escolha dois vértices consecutivos do hexágono e construa os raios da circunferência que se ligam a eles. Observe na imagem a seguir que esses raios são os segmentos OA e OB, os quais, unidos ao segmento AB, formam um triângulo:
2º – Trace o apótema do hexágono, que, na imagem acima, é o segmento AP. O apótema é um segmento de reta que liga o centro de um polígono a um de seus lados, formando com ele um ângulo reto.
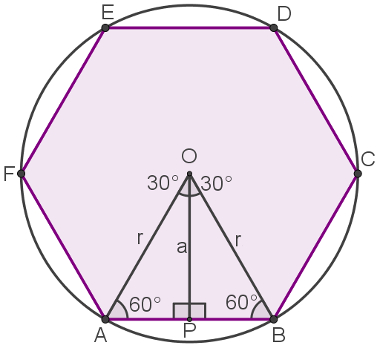
3º – Como o polígono é regular, o apótema também é mediana do lado AB e bissetriz do ângulo AÔB.
4º – Observe que o ângulo AÔB mede 60°. Isso acontece porque o polígono é regular, então, cada um de seus seis ângulos centrais é igual a 360°/6 = 60°.
5º – Como os lados AO e BO do triângulo ABO são raios da circunferência na qual o hexágono está inscrito, então, eles são congruentes. Isso significa que esse triângulo é isósceles e que os ângulos da base são iguais. Pela soma dos ângulos internos do triângulo, concluímos que cada ângulo interno de ABO mede 60°. Portanto, ele é um triângulo equilátero.
Dadas essas propriedades, colocaremos todas as medidas encontradas no triângulo ABO. Observe que, se o lado do hexágono mede l, então, o segmento PB = l/2.
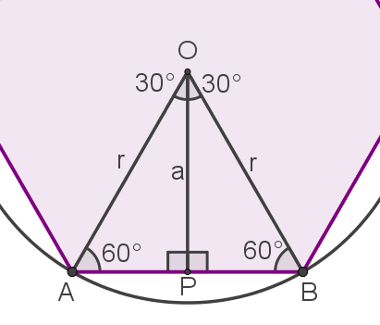
Demostração das relações métricas
Primeiramente, sabendo que o triângulo ABP é equilátero, o lado l do hexágono tem a mesma medida que o raio da circunferência. Assim:
l = r
Além disso, considere o triângulo OPB da imagem anterior e calcule o cosseno de 30°:
Cos30° = a
r
√3 = a
2 r
r√3 = a
2
a = r√3
2
Exemplo: Calcule a medida do lado e do apótema de um hexágono regular inscrito em uma circunferência de raio 10 cm.
Lado: como l = r, teremos que l = 10 cm.
Apótema: Usando a fórmula encontrada, teremos:
a = r√3
2
a = 10√3
2
a = 5√3 cm.
Artigos Relacionados

Últimas notícias
Outras matérias