Resolvendo raízes por meio da fatoração

A radiciação é a operação inversa da potenciação. Em geral, utilizamos a simbologia abaixo para representá-la:
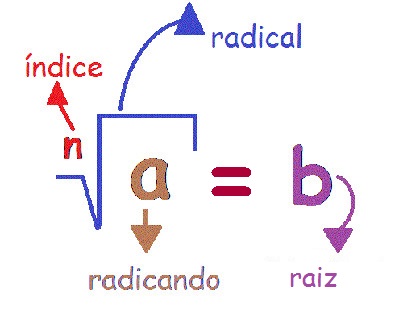
Nomes de cada elemento da radiciação
Apenas quando se tratar de raiz quadrada (índice 2) podemos deixar o espaço destinado ao índice em branco. O índice da fração indica quantas vezes é necessário multiplicar o número da potência por si mesmo até obter o valor do radicando. Por exemplo:
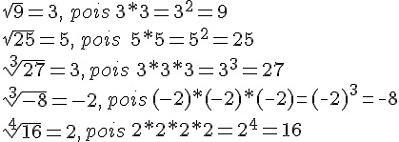
Exemplos de radiciações com índices 2, 3 e 4
Ao lidar com radicandos maiores, podem surgir dúvidas, pois o valor da raiz não aparecerá tão facilmente. Para situações como essas, devemos utilizar o processo de fatoração para obter a raiz. Vale lembrar que na fatoração há um número que deve ser dividido pelo menor número primo possível sucessivas vezes até que o quociente seja um. Vejamos como encontrar a raiz quadrada de 729:

Passo a passo da fatoração de 729
Nessa fatoração, começamos com o número do radicando, o 729, à esquerda. À direita, colocamos o menor primo que o dividirá. Novamente, à esquerda, coloca-se o número do quociente da divisão e repete-se esse processo até que o quociente seja 1. Como estamos procurando o resultado de uma raiz cujo índice é 2, agrupamos os números da direita em potências de expoente 2. Em seguida, colocamos essa multiplicação de potências dentro do radical, e aqueles números cujo o expoente é o mesmo do índice da raiz podem sair do radical sem o expoente. Vejamos outros exemplos:

Exemplos de radiciações através da fatoração
Artigos Relacionados

Últimas notícias
Outras matérias


















