Semelhança de triângulos
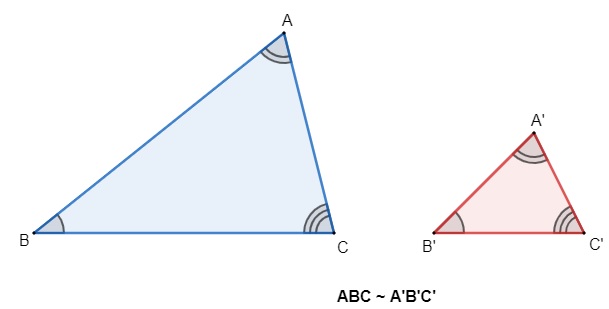
A semelhança de triângulos consiste, de modo geral, na proporção entre dois ou mais triângulos, ou seja, são proporcionais se, e somente se, todos os seus lados e ângulos internos forem proporcionais ao outro triângulo. Convenhamos que verificar todos esses elementos um a um gera um pouco de trabalho. A fim de facilitar o processo, vamos estudar os casos de semelhança nos quais é necessário verificar somente três desses elementos.
Leia também: Propriedades do triângulo equilátero
Triângulos semelhantes
Dados dois triângulos ABC e A’B’C’, vamos dizer que eles são semelhantes se, e somente se, os ângulos correspondentes são congruentes na mesma ordem, ou seja, se os ângulos são iguais e se os lados correspondentes são ordenadamente proporcionais. Veja:

Ângulos correspondentes congruentes:
A = A'
B = A'
C = A'
Lados correspondentes proporcionais:
A'B' = B'C' = A'C' = k
AB BC AC
O número k nas razões entre os lados é chamado de constante de proporcionalidade, e as razões são chamadas de razões de proporcionalidade.
Exemplo
Vamos verificar se os triângulos a seguir são proporcionais.
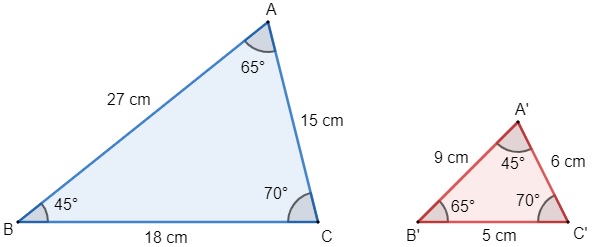
Observe que a correspondência entre os ângulos dos triângulos azul e vermelho é dada por:
A = 65° = B’
B = 45° = A’
C = 70° = C’
Veja também que o lado A’B’ está para o lado AB, que o lado B’C’ está para o lado AC e que o lado A’C’ está para o lado BC, ou seja:
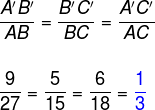
Note que, nessa ordem, podemos encontrar uma proporção entre os lados em que a constante de proporcionalidade é igual a 1/3, ou seja, para construir o triângulo A’B’C’, basta multiplicar cada lado do triângulo ABC por 1/3. Assim, temos que os triângulos são semelhantes na seguinte ordem:
ABC ~ B’A’C’
Veja também: Condição de existência de um triângulo
Teorema fundamental da semelhança de triângulos
Considere inicialmente um triângulo DEF e considere uma reta paralela GH ao lado.
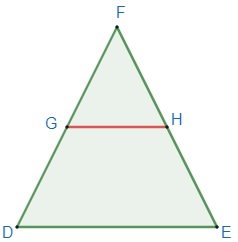
“O teorema fundamental da semelhança de triângulos afirma que toda reta paralela a um dos lados do triângulo que intercepta os outros dois lados determina um segundo triângulo semelhante ao primeiro.”
No triângulo acima, vamos ter a seguinte semelhança:
DFE ~ GFH
Exemplo
No triângulo ABC, o segmento DE é paralelo ao lado BC. Sabe-se também que AB = 8 cm, AC = 10 cm e AD = 2 cm. Determine o comprimento dos segmentos AE e EC.
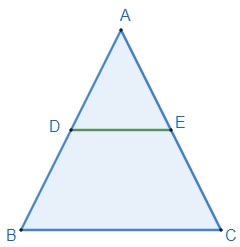
Como o segmento DE é paralelo ao lado BC do triângulo ABC, pelo teorema fundamental da semelhança de triângulos, temos que os triângulos ABC e ADE são semelhantes, logo seus lados, de modo ordenado, são proporcionais, então:
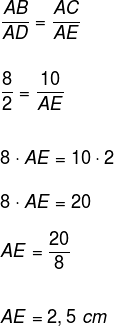
Veja também que o lado AC é dado pela soma AE + EC. Substituindo os valores de cada lado, temos:
AC = AE + EC
10 = 2,5 + EC
10 – 2,5 = EC
EC = 7,5 cm
Portanto, AE = 2,5 cm e EC = 7,5 cm.
Saiba também: Relações no triângulo retângulo
Casos de semelhança de triângulos
Vimos que, para verificar se dois triângulos são, de fato, semelhantes ,é necessário que todos os ângulos correspondentes sejam iguais e que os lados correspondentes sejam proporcionais, entretanto não é necessário verificar as seis condições. Veremos a seguir casos de semelhança que facilitam tal verificação.
-
Caso Ângulo – Ângulo (AA)
Vamos dizer que dois triângulos são semelhantes se dois ângulos de um triângulo são iguais a dois ângulos do outro triângulo.
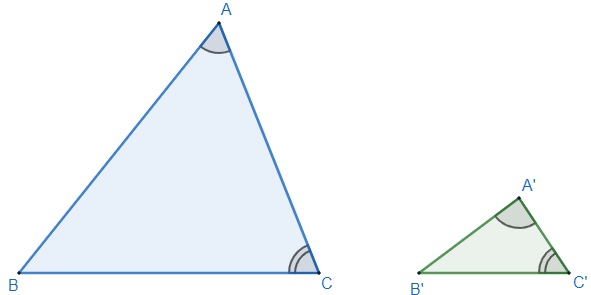
![]()
Se dois ângulos são congruentes, os triângulos são semelhantes e a volta também é verdadeira, isto é, caso dois triângulos sejam semelhantes, então podemos afirmar que dois ângulos correspondentes são iguais.
-
Caso Lado – Ângulo – Lado (LAL)
Dizemos que dois triângulos são semelhantes se dois lados são proporcionais e os ângulos entre esses lados são congruentes, isto é, iguais.
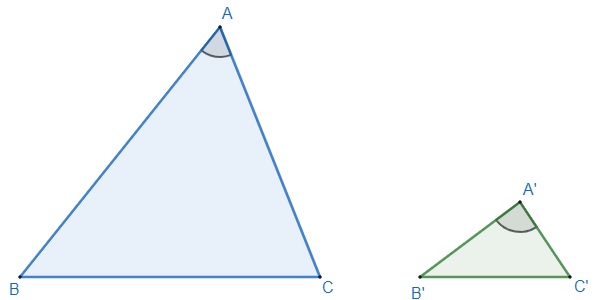
A condição para que esses dois triângulos sejam semelhantes é que a razão entre AB e A’B’ seja igual à razão entre os lados AC e A’C’, ou seja, que os lados sejam proporcionais. Além disso, o ângulo compreendido entre esses lados deve ser igual: Â = Â.
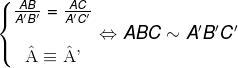
Nesse caso, também vale a volta da afirmação, ou seja, se dois triângulos são semelhantes, então podemos afirmar que dois de seus lados são proporcionais e que os ângulos entre esses lados são iguais.
-
Caso Lado – Lado – Lado (LLL)
Dois triângulos são ditos semelhantes se os três lados do primeiro triângulo são ordenadamente proporcionais aos lados do segundo triângulo.
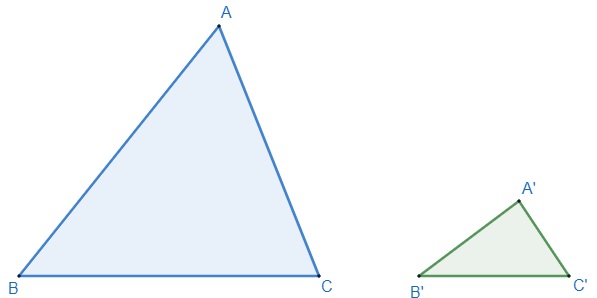
Nesse caso, para que os triângulos sejam semelhantes, os lados correspondentes devem ser iguais.
![]()
Exemplo
Considere os triângulos a seguir. Sabendo que eles são semelhantes, determine os valores de a, b e c. O perímetro do triângulo maior é igual a 84 cm.
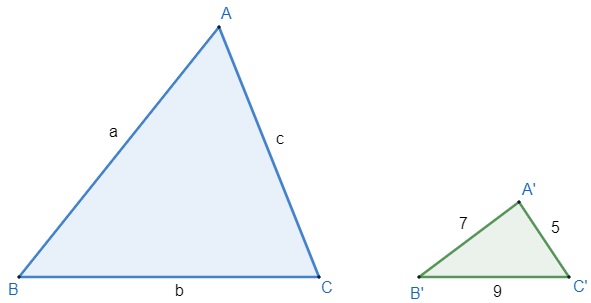
Por hipótese, os triângulos são semelhantes. Podemos dizer ainda que a semelhança é pelo caso LLL, ou seja, ABC ~ A’B’C’, portanto:
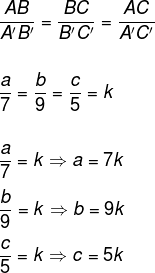
Como o perímetro do triângulo maior é igual a 84 cm, temos que:
a + b + c = 84
7k + 9k + 5k = 84
21k = 84
k =4
Substituindo os valores de k nas igualdades, temos:
a = 7 · (4) → a = 28 cm
b = 9 · (4) → b = 36 cm
c = 5 · (4) → c = 20 cm
Exercícios resolvidos sobre a semelhança de triângulos
Questão 1 – (PUC-Campinas) Os triângulos ABC e AED, representados na figura a seguir, são semelhantes, sendo os ângulos D e C congruentes.
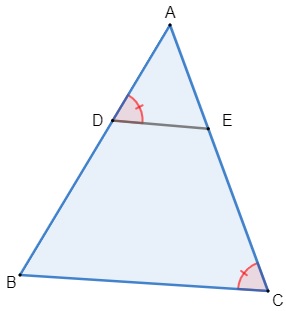
Se BC = 16 cm, AC = 20 cm, AD = 10 cm e AE = 10,4 cm, o perímetro do quadrilátero BCED, em centímetros, é:
a) 32,6
b) 36,4
c) 40,8
d) 42,6
e) 44,4
Solução
Alternativa e.
Os triângulos ABC e AED são semelhantes, logo seus lados, nessa ordem, formam uma proporção. Das propriedades de proporção, temos:
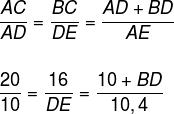
Multiplicando cruzado as duas primeiras frações, temos:
20 · DE = 10 · 16
20 · DE = 160
DE = 8 cm
Agora, multiplicando cruzado a primeira fração com a terceira, temos:
20 · 10,4 = 10 · (10 + BD)
208 = 100 + 10 · BD
10 ·BD = 208 – 100
10 · BD = 108
BD = 10,8 cm
Note que o lado AC é dado por AE + CE. Substituindo os valores conhecidos, temos:
AC = AE + CE
20 = 10,4 + CE
CE = 20 – 10,4
CE = 9,6 cm
E portanto o perímetro do quadrilátero BCED é:
BC + CE + DE + DB
16 + 9,6 + 8 + 10,8
44,4 cm
Artigos Relacionados

Últimas notícias
Outras matérias


















