Simplificação de fração
A simplificação de fração é um método utilizado para reduzir o valor do numerador e do denominador da fração sem alterar a divisão, ou seja, encontrar uma fração mais simples que represente a mesma quantidade.
Frações que representam a mesma quantidade são conhecidas como frações equivalentes, e a fração mais simples possível encontrada ao final da simplificação é conhecida como fração irredutível, logo estamos procurando a fração equivalente que seja irredutível.
Para encontrar essa fração irredutível, há dois métodos. Um deles é a realização de divisões sucessivas no numerador e no denominador. O outro é procurar o maior número que divide o numerador e o denominador ao mesmo tempo, ou seja, fazer o máximo divisor comum. Ao realizar a simplificação, já encontraremos a fração irredutível.
Leia também: Como fazer operações com frações?

O que é simplificação de fração?
O trabalho com frações é bastante comum na matemática e áreas afins, logo é recorrente que seja necessário simplificar frações para que seja mais fácil realizar contas e encontrar o resultado desejado.
Conhecemos como simplificação de uma fração a nova representação de uma fração com numerador e denominador menores, mas que ainda sim traduz a mesma quantidade. Com uma fração simplificada, fica mais fácil o trabalho com esse número em determinadas situações-problema da matemática. Em questões de vestibulares, concursos e Enem, a simplificação torna-se mais necessária ainda, já que não é permitido o uso da calculadora.
Exemplo:
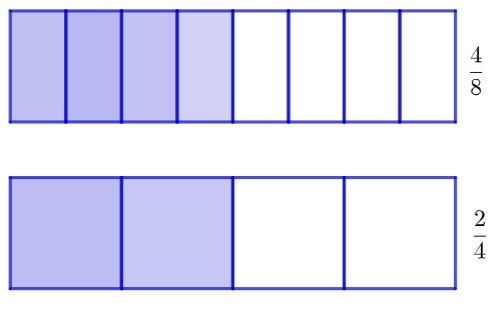
Analisando as imagens, perceba que as frações são diferentes, mas ainda sim representam a mesma quantidade, isto é, a metade da barra. Isso significa que a segunda fração (que possui numerador e denominador menores) é uma simplificação da primeira fração. Note que, se dividirmos por 2 tanto o numerador quanto o denominador da primeira fração, encontraremos a segunda.
Frações equivalentes
Assim como na imagem anterior, duas frações são conhecidas como frações equivalentes quando representam a mesma quantidade. Assim sendo, simplificar uma fração é encontrar uma fração equivalente que possui numerador e denominador menores.
Exemplos:
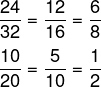
Para saber mais sobre essa propriedade dos números fracionários, acesse o nosso texto: frações equivalentes.
Métodos de simplificação de fração
São conhecidos dois métodos para encontrar as frações irredutíveis, ou seja, simplificar uma fração:
-
método das divisões sucessivas;
-
método da divisão pelo máximo divisor comum.
O primeiro costuma ser mais trabalhoso, porém é mais intuitivo. Já o segundo método é menos intuitivo, mas encontramos as frações irredutíveis com menos contas.
-
Método das divisões sucessivas
Com o objetivo de encontrar uma fração irredutível, o primeiro método, conhecido como divisões sucessivas, consiste em procurar um número que divide o numerador e o denominador simultaneamente. Ao realizar a simplificação da fração para outra com numerador e denominador menores, repetiremos o processo até que não exista nenhum divisor em comum entre eles.
Exemplo:
![]()
Note que, por mais que seja possível dividir o último denominador por dois, não é possível dividir o numerador pelo mesmo número. Como não existe mais nenhum número diferente de 1 que divida tanto o numerador quanto o denominador dessa fração, dizemos que ela é uma fração irredutível.
-
Método do máximo divisor comum
O que diferencia esse método do anterior é que não serão feitas várias divisões sucessivas, mas sim uma única divisão. Vamos escolher o maior número que divide os dois números ao mesmo tempo, que, no caso, é sempre o máximo divisor comum. Então, ao analisar o numerador e o denominador, vamos procurar o maior número que divide os dois ao mesmo tempo.
Exemplo:
![]()
O máximo divisor comum de 18 e 27 é:
D (18) = {1,2,3,6,9,18}
D(27) = {1,3,9,27}
MDC (18,27)= 9.
Então, simplificaremos o numerador e o denominador dividindo por 9.
![]()
Nesse caso, encontramos de forma direta a fração equivalente irredutível.
Veja também: Porcentagem – divisão de qualquer número por 100
Exercícios resolvidos
Questão 1 - (Enem 2016) Cinco marcas de pão integral apresentam as seguintes concentrações de fibras (massa de fibra por massa de pão):
• Marca A: 2 g de fibras a cada 50 g de pão;
• Marca B: 5 g de fibras a cada 40 g de pão;
• Marca C: 5 g de fibras a cada 100 g de pão;
• Marca D: 6 g de fibras a cada 90 g de pão;
• Marca E: 7 g de fibras a cada 70 g de pão.
Recomenda-se a ingestão do pão que possui a maior concentração de fibras.
Disponível em: www.blog.saude.gov.br. Acesso em: 25 fev. 2013.
A marca a ser escolhida será?
A) A.
B) B.
C) C.
D) D.
E) E.
Resolução
Alternativa B.
Para isso, vamos representar cada uma das frações de massa de fibra sobre massa de pão e simplificar cada uma delas.
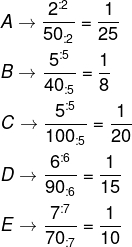
Analisando as frações, a que possui menor denominador é a que tem maior concentração de fibra, logo a resposta correta é a marca B.
Questão 2 - A fração irredutível da fração que possui denominador igual a 75 e numerador igual a 105 é:
A) 7/5
B) 5/7
C) 35/25
D) 25/35
E) 10/7
Resolução
Alternativa A.
Primeiro faremos a representação. Lembre-se de que é sempre numerador em cima e denominador embaixo. Posteriormente faremos a divisão sucessiva para encontrar a fração irredutível.
![]()
Artigos Relacionados

Últimas notícias
Outras matérias


















