Sistema linear homogêneo
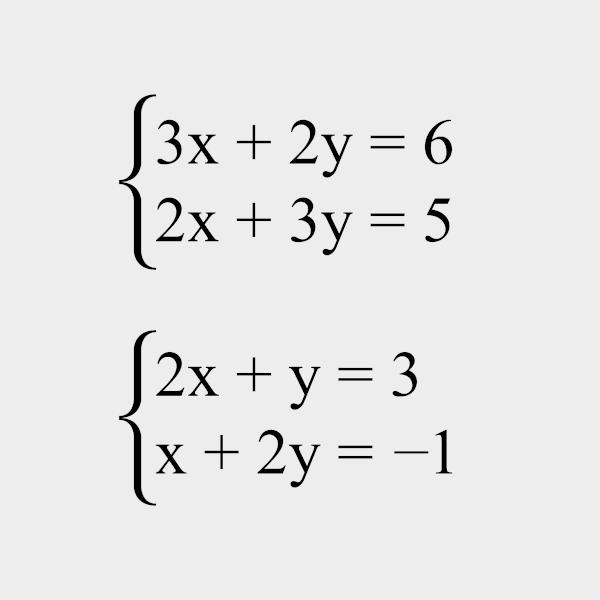
O sistema linear homogêneo ocorre quando o sistema linear tem todas as equações igualadas a zero, ou seja, o termo independente de cada uma das equações é igual a zero. Nele existe, pelo menos, uma solução, conhecida como trivial ou nula, em que todas as incógnitas são iguais a zero.
A diferença de um sistema linear homogêneo e um sistema linear não homogêneo é que, no primeiro caso, todas as equações estão igualadas a zero, já no segundo, pelo menos uma das equações é igualada a um número diferente de zero.
Um sistema homogêneo pode ter como solução somente a solução trivial, sendo um sistema possível determinado (SPD), ou mais soluções além dela, sendo um sistema possível indeterminado (SPI). Para resolvê-lo, usamos as mesmas técnicas para encontrar as soluções de um sistema qualquer, o que depende diretamente do número de equações que ele possui.
Leia também: Expressões algébricas — as expressões que têm números e letras
Resumo sobre sistema linear homogêneo
-
Conhecemos como sistema linear homogêneo aquele que tem todas as equações do 1º grau e com termo independente igual a zero.
-
De modo geral, um sistema homogêneo pode ser descrito por:
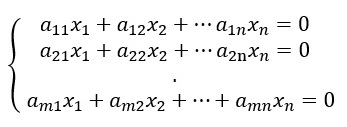
-
Todo sistema linear homogêneo tem como solução a terna (0, 0, ..., 0), conhecida como solução nula ou trivial.
-
Quando um dos termos independentes é diferente de zero, então o sistema linear não é homogêneo.
O que é um sistema linear homogêneo?
Um sistema de equação é conhecido como linear quando é composto exclusivamente por equações do primeiro grau, e como homogêneo quando o seu termo independente é igual a zero, então um sistema é classificado como linear homogêneo quando é composto por equações do 1º grau que têm termo independente igual a zero, o que significa que todas as equações serão igualadas a zero. De modo geral, representamos o sistema linear homogêneo por:
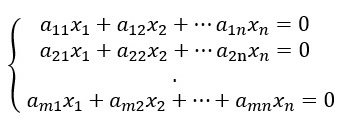
Propriedades de um sistema linear homogêneo
A principal propriedade de um sistema linear homogêneo é que ele tem como solução, pelo menos, a solução trivial, conhecida também como nula, pois todas as incógnitas iguais a 0 são solução do sistema linear homogêneo, ou seja, a terna (0, 0, ... 0).
Um sistema linear homogêneo pode ser classificado de duas formas.
-
Sistema possível determinado (SPD): quando o sistema linear tem somente a trivial como solução.
-
Sistema possível indeterminado (SPI): quando o sistema linear tem infinitas soluções.
Importante: Um sistema linear nunca será impossível, pois sabemos que ele tem, pelo menos, a solução trivial.
Diferença entre um sistema linear homogêneo e um sistema linear não homogêneo
A principal diferença entre um sistema linear homogêneo e um sistema linear não homogêneo está na sua definição em si, pois, para ser homogêneo, o termo independente tem que ser zero, já no segundo caso, é necessário que o termo independente seja diferente de zero.
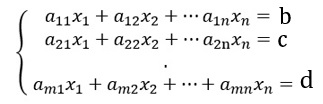
Como resolver um sistema linear homogêneo?
Para encontrar o conjunto de soluções de um sistema linear, utilizamos as mesmas técnicas para um sistema qualquer. Quando o sistema for 2x2, podemos utilizar os métodos conhecidos para resolução de sistema 2x2, como o método da adição, o da substituição ou o da igualdade. Já em um sistema 3x3, podemos utilizar as técnicas específicas para um sistema qualquer, o que é o caso do escalonamento, da regra de Cramer, entre outras.
Exemplo 1:
Encontre as soluções para o sistema.
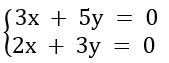
Resolução:
Analisando o sistema e utilizando o método da adição, temos que:
3x + 5y = 0 → I
2x + 3y = 0 → II
Então realizamos a multiplicação da equação I por 2, e da equação II por -3:
6x + 10y = 0 → 2I
-6x – 9y = 0 → -3II
Agora somando as linhas, temos que:
0x + y = 0
y = 0
Sabendo que y = 0, então:
2x + 3y = 0
2x + 3 \(\cdot\) 0 = 0
2x + 0 = 0
2x = 0
x = 0
Então essa equação tem somente a solução trivial.
x = 0 e y = 0
Exemplo 2:
Encontre as soluções do sistema.
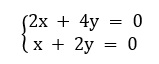
Resolução:
Utilizando o método da substituição na segunda equação, temos que:
\(x+2y=0\)
\(x=-2y\)
Agora substituindo na primeira equação:
\(2x+4y=0\)
\(2\cdot\left(-2y\right)+4y=0\)
\(-4y+4y=0\)
\(0=0\)
Quando encontramos 0 = 0, isso significa que esse sistema é um sistema possível indeterminado (SPI), ou seja, tem infinitas soluções.
As soluções devem respeitar o fato de que:
\(x=-2y\)
Por exemplo, além da solução trivial, o par ordenado (1, -2) também é solução dessa equação, ou o par (2, -4), pois o y é igual \(-2\) vezes o valor de x.
Exemplo 3:
Encontre a solução do sistema.
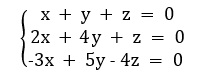
Resolução:
Analisando esse sistema, podemos perceber que ele é de ordem 3. Para resolvê-lo, utilizaremos o escalonamento.
Primeiro construímos a matriz associada ao sistema:
\(\left[\begin{matrix}1&1&1&0\\2&4&1&0\\-3&5&-4&0\\\end{matrix}\right]\)
Agora realizaremos operações algébricas entre as linhas da matriz, então faremos a operação \(L_3=3L_1+L_3\).
\(\left[\begin{matrix}1&1&1&0\\2&4&1&0\\0&8&-1\ &0\\\end{matrix}\right]\)
Agora faremos \( L_2=L_2-2L_1\).
\(\left[\begin{matrix}1&1&1&0\\0&2&-1&0\\0&8&-1\ &0\\\end{matrix}\right]\)
Agora faremos \(L_3=4L_2-L_3\).
\(\left[\begin{matrix}1&1&1&0\\0&2&-1&0\\0&0&-3\ &0\\\end{matrix}\right]\)
Então teremos o novo sistema, escalonado:
\(x+y+z=0\)
\(2y-z=0\)
\(-3z=0\)
Pela terceira equação, podemos concluir que:
\(-3z=0\)
\(z=0\)
Pela segunda equação:
\(2y-z=0\ \)
\(2y-0=0\ \)
\(2y=0\)
\(y=0\)
Por fim, pela primeira equação:
\(x+y+z=0\)
\(x+0+0=0\)
\(x=0\)
Esse é um sistema possível determinado que possui somente a solução trivial.
x = 0, y = 0 e z = 0
Veja também: Representação matricial de um sistema — a representação de um sistema em forma de matriz
Exercícios resolvidos sobre sistema linear homogêneo
Questão 1
Analise o sistema a seguir:
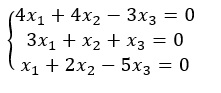
Sabendo que se trata de um sistema possível determinado, a soma das suas soluções é igual a:
A) 4
B) 3
C) 2
D) 1
E) 0
Resolução:
Alternativa E
Como o sistema é homogêneo, ele tem como solução a solução trivial (0, 0, 0). Como ele é possível e determinado, essa é a única solução, então temos que 0 + 0 + 0 = 0.
Questão 2
Analise o sistema a seguir:
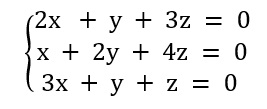
Podemos afirmar que:
I. Esse sistema é um sistema linear homogêneo.
II. Uma solução desse sistema é a solução trivial.
III. O sistema é um sistema impossível.
Marque a alternativa correta.
A) Somente a I é falsa.
B) Somente a II é falsa.
C) Somente a III é falsa.
D) Todas são verdadeiras.
Resolução:
Alternativa C
I. Esse sistema é um sistema linear homogêneo. (verdadeira)
Note que os termos independentes desse sistema são todos iguais a zero, e que todas as sentenças são equações do 1º grau, o que faz com que ele seja um sistema linear homogêneo.
II. Uma solução desse sistema é a solução trivial. (verdadeira)
Todo sistema linear homogêneo tem como solução a trivial.
III. O sistema é um sistema impossível. (falsa)
O sistema homogêneo sempre terá a solução trivial, logo, ele não pode ser classificado como um sistema impossível.
Artigos Relacionados

Últimas notícias
Outras matérias


















