Regra de Cramer

Regra de Cramer é o método utilizado para encontrar as soluções de um sistema linear. Ela é aplicada principalmente em sistemas lineares 3x3, ou seja, que possuem três equações e três incógnitas.

Para aplicarmos essa regra em um sistema linear, é necessário encontrar as matrizes associadas ao sistema, calcular o determinante das matrizes e utilizar a razão entre os determinantes para chegar ao valor de cada uma das incógnitas.

Leia também: Teorema de Laplace — método para calcular o valor do determinante de matrizes quadradas

Resumo sobre a regra de Cramer

• A regra de Cramer é usada na resolução de sistemas lineares.

• Utilizamos as matrizes associadas ao sistema para aplicar a regra de Cramer.

• Dado um sistema de equações, a regra de Cramer define que:

\(x=\frac{D_x}{D},\ \ \ \ \ \ y=\frac{D_y}{D},\ \ \ e\ \ \ \ z=\frac{D_z}{D}\)

• D, D_x, D_y e D_z são os determinantes das matrizes associadas ao sistema. 

Videoaula sobre a regra de Cramer

O que é a regra de Cramer?

Regra de Cramer é um método utilizado para encontrar o conjunto solução de um sistema de equação linear possível determinado. Essa regra utiliza o determinante das matrizes associadas ao sistema para encontrar as soluções do sistema. O método é aplicado principalmente em sistemas lineares que possuem 3 incógnitas e 3 equações, mas pode ser empregado também em sistemas lineares 2 por 2.

Como usar a regra de Cramer

A seguir, temos um sistema linear com 3 linhas e 3 colunas:

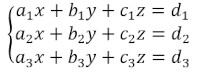
No sistema, é possível aplicar a regra de Cramer. Para isso, de início calcularemos o determinante da matriz incompleta D.

\(D\ =\ \left|\begin{matrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\\\end{matrix}\right|\)

Também calcularemos D_x, que é o determinante da matriz incompleta, substituindo a primeira coluna pelos termos independentes d₁, d₂ e d₃.

\(D_x=\left|\begin{matrix}d_1&b_1&c_1\\d_2&b_2&c_2\\d_3&b_3&c_3\\\end{matrix}\right|\)

\(D_y\) e \(D_z\) são os determinantes das matrizes incompletas, que substituem, respectivamente, a segunda e a terceira coluna pelos termos independentes.

\(D_y=\left|\begin{matrix}a_1&d_1&c_1\\a_2&d_2&c_2\\a_3&d_3&c_3\\\end{matrix}\right|\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ D_z=\left|\begin{matrix}a_1&b_1&d_1\\a_2&b_2&d_2\\a_3&b_3&d_3\\\end{matrix}\right|\)

Pela regra de Cramer, conhecendo os valores dos determinantes anteriores, temos que:

\(x=\frac{D_x}{D},\ \ \ \ \ \ y=\frac{D_y}{D},\ \ \ e\ \ \ \ z=\frac{D_z}{D}\)

Logo, perceba que quando o sistema possui solução, é possível encontrar os valores de x, y e z utilizando a regra de Cramer.

Leia também: Regra de Sarrus — método para calcular o determinante de matrizes de ordem 2 e 3

Solução de sistemas usando a regra de Cramer

Vejamos, a seguir, a aplicação da regra de Cramer para sistemas lineares 2x2 e 3x3.

• Solução de sistemas 2x2

Quando o sistema linear é 2x2, há apenas duas variáveis, como no exemplo:

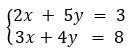
Para resolver esse sistema aplicando a regra de Cramer, de início calcularemos o determinante D:

\(D\ =\left|\begin{matrix}2&5\\3&4\\\end{matrix}\right|\ \)

\(D\ =\ 2\ \cdot4\ -\ 3\ \cdot5\ \)

\(D\ =\ 8\ -\ 15\)

\(D\ =\ -\ 7\)

Agora, calcularemos \(D_x\ e\ D_y\):

\(D_x=\left|\begin{matrix}3&5\\8&4\\\end{matrix}\right|\)

\(D_x=3\cdot4-8\cdot5\)

\(D_x=12-40\)

\(D_x=-28\)

\(D_y=\left|\begin{matrix}2&3\\3&8\\\end{matrix}\right|\)

\(D_y=2\cdot8-3\cdot3\)

\(D_y=16-9\)

\(D_y=7\)

Como conhecemos os valores de \(D,D_x\ e\ D_y\), podemos encontrar o valor de cada uma das incógnitas:

\(x=\frac{D_x}{D}=\frac{-28}{-7}=4\)

\(y=\frac{D_y}{D}=\frac{-7}{7}\ =\ -\ 1\ \)

• Solução de sistemas 3x3

Vejamos agora um exemplo da regra de Cramer aplicada a um sistema 3x3.

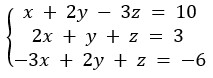
Pela regra de Cramer, temos que:

\(D\ =\ \left|\begin{matrix}1&2&-3\\2&1&1\\-3&2&1\\\end{matrix}\right|\)

\(D=1\cdot1\cdot1+2\cdot1\cdot\left(-3\right)+\left(-3\right)\cdot2\cdot2-\left(-3\right)\cdot1\cdot\left(-3\right)-1\cdot2\cdot1-1\cdot2\cdot2\)

\(D\ =\ 1\ -\ 6\ -12\ -9\ -2-4\)

\(D\ =\ -32\)

Calculando \(D_x\):

\(D_x=\left|\begin{matrix}10&2&-\ 3\\3&1&1\\-6&2&1\\\end{matrix}\right|\)

\(D_x=10\cdot1\cdot1+2\cdot1\cdot\left(-6\right)+\left(-3\right)\cdot3\cdot2-\left(-6\right)\cdot1\cdot\left(-3\right)-2\cdot1\cdot10–1⋅3⋅2=-64\)

Calculando \(D_y\):

\(D_y=\left|\begin{matrix}1&10&-\ 3\\2&3&1\\-3&-6&1\\\end{matrix}\right|\)

\(D_y=1\cdot3\cdot1+10\cdot1\cdot\left(-3\right)+\left(-3\right)\cdot2\cdot\left(-6\right)-\left(-3\right)\cdot3\cdot\left(-3\right)-1\cdot1\cdot\left(-6\right)-10\cdot2\cdot1\)

\(D_y=3-30+36-27+6-20\)

\(D_y=-32\)

Calculando \(D_z\):

\(D_z=\left|\begin{matrix}1&2&10\\2&1&3\\-3&2&-\ 6\\\end{matrix}\right|\)

\(D_z=1\cdot1\cdot\left(-6\right)+2\cdot3\cdot\left(-3\right)+10\cdot2\cdot2-10\cdot1\cdot\left(-3\right)-1\cdot3\cdot{2}-\ 2\cdot2\cdot\left(-6\right)\)

\(D_z=-6-18+40+30-6+24\)

\(D_z=64\)

Calculando os valores de x, y e z:

\(x=\frac{D_x}{D}=\frac{-64}{-32}=2\)

\(y=\frac{D_y}{D}=\frac{-32}{-32}=1\)

\(z=\frac{D_z}{D}=\frac{64}{-32}=-2\)

Então, temos que \(x=2\), \(y=1\) e \(z=-\ 2.\).

Leia também: Como resolver matrizes e determinantes?

Exercícios resolvidos sobre regra de Cramer

Questão 1

Sobre a Regra de Cramer, marque a alternativa correta:

A) A regra de Cramer é um método desenvolvido para calcular determinantes de matrizes de ordem 2 e ordem 3.

B) A regra de Cramer é um método desenvolvido para calcular a matriz inversa quando ela existir.

C) A regra de Cramer é um método desenvolvido para calcular uma matriz transposta.

D) A regra de Cramer é um método desenvolvido para calcular as soluções de sistemas lineares.

Resolução:

Alternativa D

A regra de Cramer foi desenvolvida como um método que nos auxilia a calcular soluções de sistemas lineares.

Questão 2

Analisando o exemplo a seguir, podemos afirmar que a soma dos valores de x + y que satisfazem o sistema é igual a:

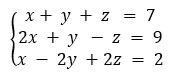
A) 4

B) 5

C) 6

D) 7

E) 8

Resolução:

Alternativa C

Utilizaremos regra de Cramer para encontrar o valor de x + y.

Primeiramente, calcularemos o valor de D:

D = \(\left|\begin{matrix}1&1&1\\2&1&-1\\1&-2&2\\\end{matrix}\right|\)

D = \(1\cdot1\cdot2+1\cdot\left(-1\right)\cdot1+1\cdot2\cdot\left(-2\right)-1\cdot1\cdot1-1\cdot\left(-1\right)\cdot\left(-2\right)-1\cdot2\cdot2\)

D = \(2\ -\ 1\ -\ 4\ -\ 1\ -\ 2\ -\ 4\)

D = - 10

Sabemos que x + y + z = 7 analisando a primeira linha do sistema. Assim, se encontrarmos o valor de z, encontraremos o valor de x + y. Logo, calculando \(D_z\):

\(D_z=\left|\begin{matrix}1&1&7\\2&1&9\\1&-2&2\\\end{matrix}\right|\)

\(D_z=1\cdot1\cdot2+1\cdot9\cdot1+7\cdot2\cdot\left(-2\right)-7\cdot1\cdot1-1\cdot9\cdot\left(-2\right)-1\cdot2\cdot2\)

\(D_z=2+9-28-7+18-4\)

\(D_z=-10\)

Então, temos que:

\(z=\frac{D_z}{D}=\frac{-10}{-10}=1\)

Sabendo que z = 1:

\(x\ +\ y\ +\ z\ =\ 7\)

\(x\ +\ y\ +\ 1\ =\ 7\)

\(x\ +\ y\ =\ 7\ -\ 1\ \)

\(x\ +\ y\ =\ 6\)