Tabelas de razões trigonométricas
As tabelas trigonométricas relacionam um ângulo aos seus respectivos valores de seno, cosseno e tangente. Elas foram criadas para facilitar quaisquer cálculos envolvendo trigonometria, pois, fazendo uso de uma dessas tabelas, basta procurar os valores numéricos de seno, cosseno e tangente referentes a um ângulo qualquer.
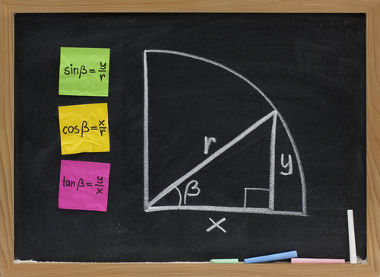
Seno, cosseno e tangente são resultados da divisão dos comprimentos de dois lados de um triângulo retângulo. Para definir essas divisões, é necessário saber que, em um triângulo retângulo, o lado oposto ao ângulo de 90º é chamado de hipotenusa e que os outros dois lados são chamados de catetos.
Tomando o ângulo θ de um triângulo retângulo, sendo θ diferente de 90º, definiremos:
Senθ = Cateto oposto a θ
hipotenusa
cosθ = Cateto adjacente a θ
hipotenusa
tgθ = Cateto oposto a θ
Cateto ajacente a θ
Essas razões funcionam em qualquer triângulo retângulo que possua um ângulo igual a θ, independentemente do comprimento dos lados desses triângulos, em virtude da semelhança de triângulos pelo caso ângulo – ângulo.
A primeira tabela trigonométrica envolve apenas ângulos notáveis, isto é, os ângulos de 30º, 45º e 60º.
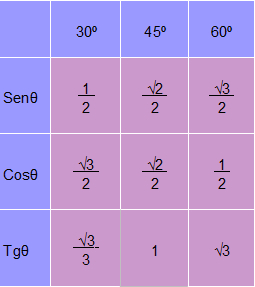
Tabela dos valores numéricos de seno, cosseno e tangente dos ângulos notáveis
Geralmente os professores usam uma música para que os alunos jamais se esqueçam dessa tabela. A canção é a seguinte:
“um, dois, três.
Três, dois, um.
Tudo sobre dois,
só não tem raiz o um!”
Repare que cada verso é um passo para a construção dessa tabela. Escreve-se 1, 2, 3 na primeira linha; 3, 2, 1 na segunda; divide-se tudo por 2, e o único numerador que não possui raiz é o 1. A linha referente à tangente é obtida pela divisão dos valores de seno por cosseno.
Caso os ângulos sejam diferentes de 30º, 45º ou 60º, pode-se utilizar a tabela seguinte, que aproxima os valores de seno, cosseno e tangente de cada ângulo agudo.
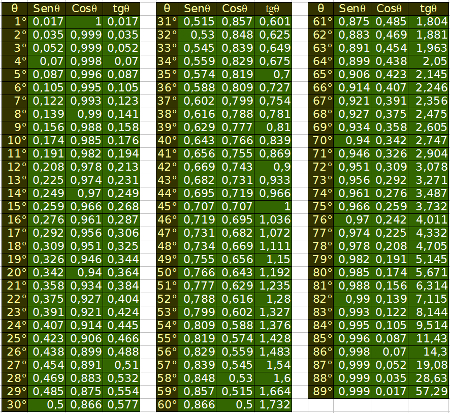
Tabela trigonométrica com todos os ângulos agudos
Exemplo: Calcule o valor de x no triângulo abaixo.
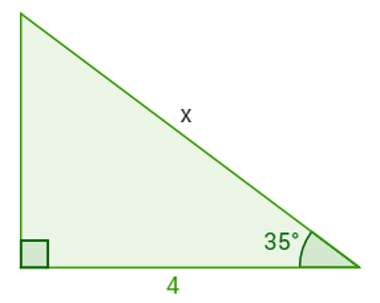
Triângulo retângulo com um ângulo agudo de 35°
Para calcular o valor de x na figura acima, basta utilizar a noção de cosseno, já que as medidas que dispomos são de um ângulo agudo de um triângulo retângulo, do cateto adjacente a esse ângulo e da hipotenusa (é a medida que queremos descobrir).
Cosθ = Cateto adjacente
hipotenusa
Cos35° = 4
x
Observe na tabela que Cos35° = 0,819. Substitua esse valor na expressão acima e utilize regra de três para calcular o valor de x.
Cos35° = 4
x
0,819 = 4
x
0,819x = 4
x = 4
0,819
x = 4,88
Logo, a medida de x é 4,88.
Artigos Relacionados

Últimas notícias
Outras matérias


















