Teoria dos conjuntos
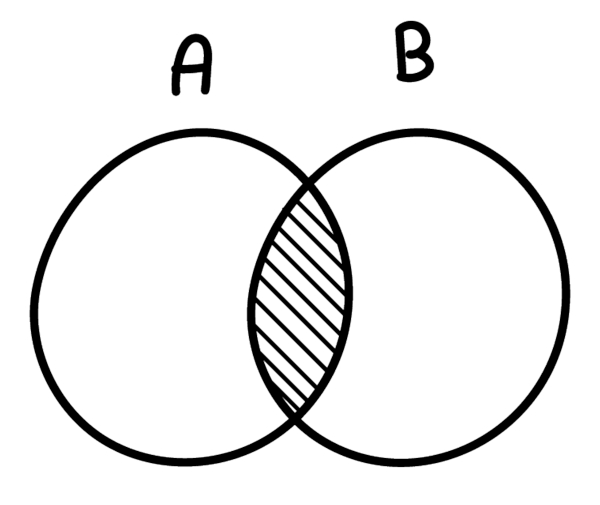
A teoria dos conjuntos é estudada na álgebra, que é uma área da Matemática. Um conjunto é um agrupamento de elementos que possuem uma determinada característica em comum, como o conjunto de vogais, conjunto de números, conjunto de pessoas, entre outros.
Existem algumas relações importantes na teoria dos conjuntos, como pertinência, inclusão, entre outras, e podemos realizar operações entre eles, como união, intersecção e diferença. Vale dizer ainda que um conjunto pode ser representado por meio do chamado diagrama de Venn, fundamental para o estudo das operações entre os conjuntos.
Leia também: Conjuntos e seus elementos — relações e representações
Resumo sobre a teoria dos conjuntos
-
A teoria dos conjuntos é a área da Matemática que estuda as características e propriedades dos conjuntos.
-
Um conjunto é formado por elementos que possuem uma mesma característica.
-
Quando o elemento está em um conjunto, dizemos que ele pertence ao conjunto. Caso contrário, dizemos que ele não pertence ao conjunto.
-
Quando todos os elementos do conjunto A são também elementos do conjunto B, dizemos que o conjunto A está contido no conjunto B.
-
Conhecemos como subconjunto de A um conjunto que está contido no conjunto A.
-
Existem alguns casos particulares de conjunto:
-
Conjunto vazio: não possui elementos.
-
Conjunto unitário: possui um único elemento.
-
Conjunto universo: contém todos os outros conjuntos.
-
Conjunto complementar: o complementar de um conjunto A é composto por todos os elementos do universo que não pertencem ao conjunto A.
-
-
Podemos realizar operações entre conjuntos. São elas a união, a intersecção e a diferença.
Notação e representação dos conjuntos
A representação de um conjunto é feita utilizando uma letra maiúscula do nosso alfabeto, e os elementos do conjunto estão sempre entre chaves e separados por vírgula. Por exemplo, o conjunto A formado pelas vogais do alfabeto é o conjunto A = {a, e, i, o, u}. O conjunto M é o conjunto dos números múltiplos de 5: M = {0, 5, 10, 15, 20, 25...}
Diagrama de Venn
O diagrama de Venn é uma outra forma de representar os conjuntos. Ele é muito utilizado para resolver problemas envolvendo operações entre conjuntos, pois facilita a visualização dos elementos.
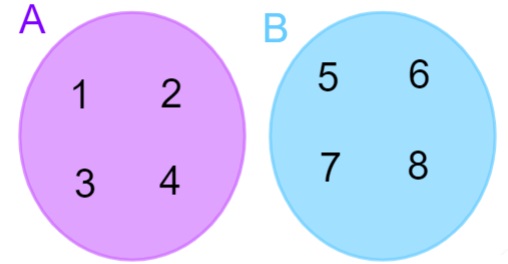
Veja a seguir a representação dos conjuntos A = {1, 2, 3, 4} e B = {5, 6, 7, 8} no diagrama de Venn.
Relação de pertinência
Um conjunto é composto por elementos. Quando o elemento está no conjunto, dizemos que esse elemento pertence ao conjunto. O símbolo para representar isso é \(\in\) (lê-se: pertence). Quando um elemento não está no conjunto, dizemos que esse elemento não pertence ao conjunto. A não pertinência é representada por \(\notin\).
Exemplos:
-
a \(\in\) ao conjunto das vogais {a, e, i, o, u}.
-
2 \(\in\) ao conjunto dos números pares.
-
a \(\notin\) ao conjunto das consoantes {b, c, d, f, g, h, j, k, l, m, n, p, q, r, s, t, v, w, x, y, z}.
-
2 \(\notin\) ao conjunto dos números ímpares.
Relação de continência
Quando fazemos a comparação de dois conjuntos, notamos uma relação importante chamada de continência. Dizemos que um conjunto A está contido no conjunto B quando todos os elementos do conjunto A são também elementos do conjunto B. Podemos dizer também que o conjunto B contém o conjunto A. Para expressar essa relação, utilizamos os símbolos a seguir:
⊃ — contém
⊂ — está contido
⊅ — não contém
⊄ — não está contido
Exemplo:
Dados os conjuntos A = {0, 5, 10} e B = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, podemos dizer que:
B ⊃ A (B contém A) ou também que A ⊂ B (A está contido em B).
Subconjuntos
Chamamos de subconjunto de um conjunto B o conjunto A que está contido no conjunto B. Em um determinado conjunto, podemos ter vários subconjuntos.
Exemplo:
B = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
Alguns subconjuntos de B são:
A = {1, 2, 3, 4, 5}
C = {2, 4, 6, 8, 10}
D = {10}
Leia também: Subconjuntos e relação de inclusão
Casos particulares de conjuntos
-
Conjunto vazio
Um conjunto é conhecido como vazio quando ele não possui nenhum elemento. Ele pode ser representado por { } ou pelo símbolo \(\emptyset\) — ambos possuem o mesmo significado. O conjunto vazio está contido em todo e qualquer conjunto.
-
Conjunto unitário
Conhecemos como conjunto unitário aquele que possui somente um único elemento pertencente a ele — por exemplo, os conjuntos A = {0}, B ={1} e C = {2}.
-
Conjunto universo
O conjunto universo é definido como o conjunto formado por todos os elementos que devem ser considerados para uma determinada situação. Todo elemento pertence ao conjunto universo e todo conjunto está contido nele.
Operações entre os conjuntos
Existem três importantes operações entre os conjuntos: a união, a intersecção e a diferença entre conjuntos. Veja a seguir cada uma delas.
-
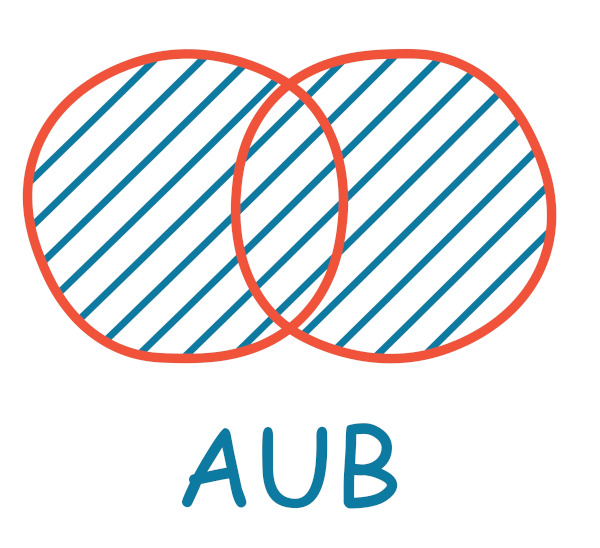
União de conjuntos
Conhecemos como união de dois (ou mais) conjuntos o conjunto formado por todos os elementos de ambos. Para representar a união de dois conjuntos, utilizamos a notação A \(\cup\) B (lê-se: A união com B).
Exemplo:
Seja A = {2, 4, 6, 8, 10} e B = {1, 2, 3, 4, 5, 6}, a união entre ambos será: A \(\cup\) B = {1, 2, 3, 4, 5, 7, 8, 10}
Veja a seguir a representação da união no diagrama de Venn:
-
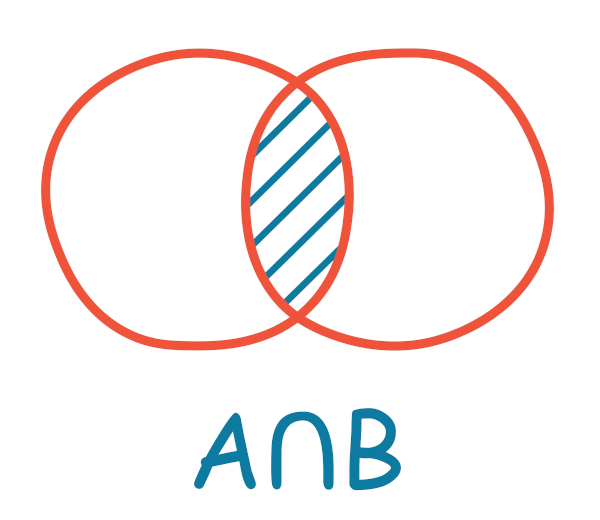
Intersecção de conjuntos
A intersecção de dois (ou mais) conjuntos é formada pelos elementos que pertencem a ambos ao mesmo tempo. A intersecção é representada por A \(\cap\) B (lê-se: A intersecção com B).
Exemplo:
Seja A = {2, 4, 6, 8, 10} e B = {1, 2, 3, 4, 5, 6}, temos que: A \(\cap\) B = {2, 4, 6}.
Veja a seguir a representação da intersecção de dois conjuntos no diagrama:
-
Diferença entre conjuntos
A diferença entre os conjuntos A e B é representada por A – B. Calcular essa diferença é encontrar os elementos que pertencem exclusivamente ao conjunto A, ou seja, pertencem ao A e não pertencem ao B.
Exemplo:
Seja A = {2, 4, 6, 8, 10} e B = {1, 2, 3, 4, 5, 6}, a diferença entre os conjuntos A e B é igual a:
A – B = {8, 10}
-
-
Conjunto complementar
-
O conjunto complementar é um caso especial de diferença entre dois conjuntos. Dado um universo U, o conjunto complementar de A é denotado por Ac é igual a U – A, ou seja, o conjunto de elementos que estão no universo, mas não pertencem ao conjunto A.
Exemplo:
Seja U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, e dado o conjunto A = {2, 4, 6, 8, 10}, o conjunto complementar de A, ou seja, AC é igual a U – A = {1, 3, 5, 7, 9}.
Confira na nossa videoaula: Operações entre conjuntos
Exercícios resolvidos sobre teoria dos conjuntos
Questão 1
(Unesc 2022) Analisando o diagrama lógico dado abaixo, podemos afirmar que o conjunto que representa o elemento X, que faz parte da operação lógica (A ^ B), é o:
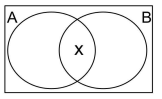
A) A ∈ B
B) A ⊂ B
C) A ∪ B
D) A ⊃ B
E) A ∩ B
Resolução:
Alternativa E
Essa região é a intersecção dos dois conjuntos, e a intersecção é representada por A ∩ B (A intersecção com B).
Questão 2
(Fafipa 2014) Considere os conjuntos A = {3, 6, 11, 13, 21} e B = {2, 3, 4, 6, 9, 11, 13, 19, 21, 23, 26}. Sobre os conjuntos A e B, podemos afirmar que:
A) A ⊂ B
B) 9 ∉ B
C) 17 ∈ A
D) A ⊃ B
Resolução:
Alternativa A
Analisando os conjuntos, é possível perceber que todos os elementos do conjunto A pertencem ao conjunto B. Quando isso acontece, dizemos que o conjunto A está contido no conjunto B, então temos que A ⊂ B.
Artigos Relacionados

Últimas notícias
Outras matérias


















