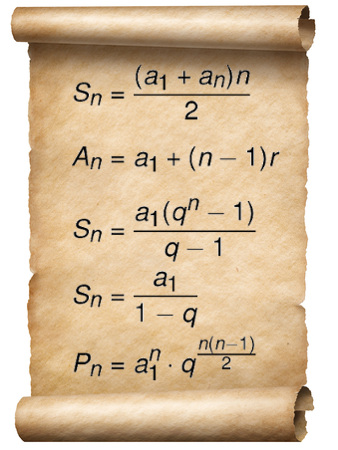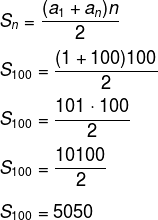Três erros mais cometidos em progressões no Enem
No Exame Nacional do Ensino Médio (Enem), são muito comuns questões envolvendo progressões conhecidas como PA e PG. Neste artigo, veja quais são os erros mais comuns cometidos por alunos que não conseguem acertar essas questões e aprenda uma forma de não cometer tais erros, obtendo mais chances de sucesso nesse exame.
Apenas para lembrar o que é uma progressão e o que são PA e PG, suas definições serão expostas a seguir.
Veja também: Soma de Gauss
Definições básicas
Uma progressão é uma sequência numérica onde a ordem dos números apresenta algum tipo de padrão.
Uma progressão é chamada progressão aritmética (PA) quando cada um dos seus elementos é igual à soma de seu antecessor com uma constante, que é a mesma para qualquer elemento da PA. Em outras palavras, uma sequência numérica é PA quando a diferença entre dois de seus termos consecutivos é sempre igual a uma constante, que é chamada de razão e representada pela letra r.
Uma progressão é chamada progressão geométrica (PG) quando cada um dos seus termos é igual ao produto do anterior por uma constante, também chamada de razão e representada pela letra q.
Primeiro erro
É muito comum achar entre os estudantes aqueles que erram qualquer cálculo matemático por falta de atenção. Frequentemente, encontramos soluções com uso de fórmulas e de conhecimentos matemáticos corretos, mas com um erro simples ao final. Por exemplo: um erro ao colocar o sinal da última parte do exercício invertido ou ao fazer a penúltima multiplicação como se fosse uma soma. Por exemplo: após toda a parte mais difícil do exercício, que envolve o conceito matemático da PA ou da PG, o aluno faz: 4·4 = 8.
É importante que o aluno faça uma boa leitura do exercício, assinalando o que foi solicitado nele. Isso porque também é frequente deixar passar uma informação indispensável para a solução do exercício. É comum que o exercício solicite algo diferente do “valor de x”. Por exemplo: qual é a metade da soma dos termos da PA…
Em questões de múltipla escolha, o resultado da soma dos termos dessa PA também estará entre as alternativas, mas será incorreta.
Veja também: Trabalhando ao mesmo tempo com PA e PG
Segundo erro
Também é comum que os estudantes não se lembrem das fórmulas usadas nas progressões e não conheçam uma maneira de chegar a elas. Essas fórmulas são: fórmula do termo geral da PA, fórmula do termo geral da PG, fórmula da soma dos termos da PA, fórmula da soma dos termos de uma PG finita, fórmula da soma dos termos de uma PG infinita e fórmula do produto dos termos de uma PG finita.
Por isso, aconselhamos os alunos a estudar os meios usados para encontrar tais fórmulas. Esses meios também servem para resolver alguns tipos de exercícios envolvendo progressões – então esse estudo é útil de diversas formas.
Alunos que conhecem esses métodos não precisam se apegar a fórmulas e acabam desenvolvendo muito mais o raciocínio lógico. Além disso, esse tipo de conhecimento demora mais para ser esquecido. A fórmula decorada, por sua vez, é esquecida facilmente.
Terceiro erro
O terceiro erro mais comum é não pensar que algumas progressões podem não estar expressas de maneira óbvia. É como se o exercício se referisse a uma progressão geométrica ou aritmética disfarçada.
Exemplo: Qual é o centésimo termo da sequência A = (1, 3, 6, 10, 15, …)?
Solução: note que cada termo dessa sequência pode ser obtido pela soma de termos de progressões aritméticas de números naturais, com primeiro termo igual a 1, razão igual a 1 e número de termos igual à posição do número da sequência. Em outras palavras, os termos da sequência A são:
a1 = 1 = 1
a2 = 3 = 1 + 2
a3 = 6 = 1 + 2 + 3
a4 = 10 = 1 + 2 + 3 + 4
a5 = 15 = 1 + 2 + 3 + 4 + 5
…
A quantidade de termos somados é igual ao índice n, ou seja, à posição ocupada pelo termo da sequência A. Para descobrir o centésimo termo, basta fazer a soma de todos os números naturais de 1 até 100. Esse conjunto forma uma PA finita, de 100 termos, com razão 1 e primeiro termo também 1.
Artigos Relacionados

Últimas notícias
Outras matérias