Triângulo de Pascal
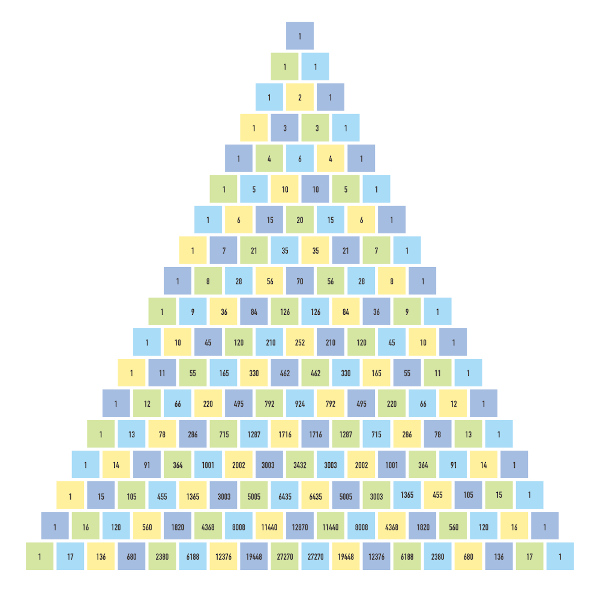
O triângulo de Pascal é uma ferramenta utilizada para encontrar o valor de combinações estudadas na análise combinatória. Ao longo da história, ele já recebeu outros nomes, como triângulo de Tartaglia e triângulo aritmético. Atualmente o nome mais comum dado a ele é triângulo de Pascal, uma homenagem ao matemático que fez várias contribuições durante o estudo desse triângulo, descobrindo as suas principais propriedades e aplicações.
A construção do triângulo de Pascal é realizada seguindo uma lógica herdada das suas propriedades, possuindo aplicações para encontrar as combinações da análise combinatória. Ele é utilizado também para encontrar os coeficientes binomiais, ou seja, auxilia no cálculo de um binômio de Newton.
Leia também: Análise combinatória — área de estudo matemático associada a regras de contagem
Resumo sobre triângulo de Pascal
-
É formado pelas combinações, e dividido por linhas e colunas.
-
É utilizado para resolver problemas de combinação.
-
Uma das suas aplicações é na resolução de binômios de Newton.
Construção do triângulo de Pascal
O triângulo de Pascal é dividido por linhas e colunas, começando sempre da linha zero e da coluna zero. Ele é formado por combinações, ou seja, na linha 0 e coluna 0, teremos a combinação de 0 elemento tomado de 0 em 0, na linha 1 coluna 1, teremos a combinação de 1 elemento tomado de 1 em 1, e assim por diante. Podemos construir quantas linhas forem necessárias seguindo essa mesma lógica.

Esse é o triângulo de Pascal até a linha 5, mas, se necessário, podemos construir mais linhas.
Acontece que, para construir o triângulo, substituiremos as combinações pelos seus resultados, e para isso, primeiro, lembraremos que a combinação de um número qualquer tomado de 0 em 0 é sempre igual a 1. Além disso, a combinação de um número n tomado de n em n também é sempre igual a 1, então temos que:

Agora, para encontrar as demais combinações sem ter a necessidade de resolver a combinação, começaremos com o termo que está na linha 2 e coluna 1, ou seja, combinação de 2 termos tomados de 1 em 1.
Para encontrar o valor desse termo, vamos realizar a soma do termo que está na mesma coluna e na linha anterior à dele, com o termo que está a uma linha e uma coluna anterior a ele, como na imagem a seguir:

Sabemos que 1 + 1 = 2, então, temos que:

Agora, para encontrar os termos da terceira linha, vamos repetir esse processo. Então, a combinação de 3 tomados de 1 a 1 é igual à soma de 1 + 2, assim como a combinação de 3 tomados de 2 em 2 é igual a 2 + 1:

Dessa forma, conseguimos encontrar os termos da terceira linha:

Para encontrar os demais termos, basta repetir esse processo. Então, o triângulo de Pascal, até a sua linha 5, ficará da seguinte maneira:

Leia também: Você sabe como resolver anagramas pelo princípio fundamental da contagem?
Propriedades do triângulo de Pascal
Quando realizamos a construção do triângulo de Pascal, é possível encontrar algumas relações entre os valores das linhas, das colunas e das diagonais. Vejamos, a seguir, as principais propriedades do triângulo de Pascal.
-
1ª propriedade: relação de Stifel.
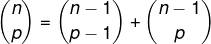
Com a utilização dessa propriedade, é possível construir o triângulo como fizemos anteriormente, ou seja, um termo qualquer é igual à soma do termo que está na linha acima dele com o termo que está acima dele na coluna anterior.
-
2ª propriedade: a soma dos termos da coluna p até determinada linha n é igual ao termo que está na linha n + 1 posterior e coluna p + 1 posterior, como mostra na imagem a seguir.
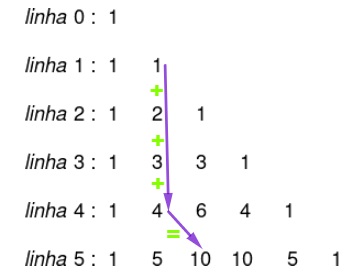
-
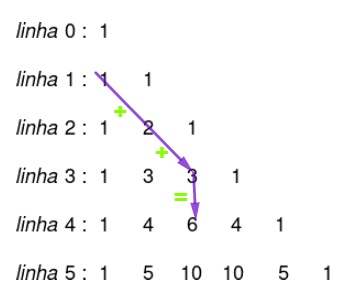
3ª propriedade: a soma de uma diagonal que vai até o termo que se encontra na coluna p e linha n é igual ao termo que está na mesma coluna p e na linha n + 1:
-
4ª propriedade: a soma dos termos de determinada linha n é calculada por:
|
Sn = 2n |
Exemplo:

Binômio de Newton
O binômio de Newton é um método que utilizamos para calcular potências de um binômio, descrito por:
![]()
Acontece que o triângulo de Pascal nos auxilia a resolver os problemas envolvendo o binômio de Newton. Com o triângulo, não é necessário realizar o cálculo das combinações, basta consultá-lo para encontrar o que conhecemos como coeficiente binomial.
-
Coeficiente binomial
O coeficiente binomial nada mais é que as combinações que acompanham cada um dos termos do binômio. Para resolver problemas envolvendo binômio de Newton, bastar verificar à qual linha do triângulo de Pascal aquela potência se refere, por exemplo:
Calcule (a + b)³.
Analisando a linha 3, ela é composta pelos números 1, 3, 3 e 1, então, temos que:
(a + b)³ = 1a³ + 3a²b + 3ab² + 1b³
Sendo assim, não é necessário calcular os coeficientes binomiais, mas apenas consultar a linha a que essa potência se refere.
Leia também: Permutação simples — tipo de agrupamento estudado na análise combinatória
Exercícios resolvidos sobre triângulo de Pascal
Questão 1
Dado o binômio (x + y)8, a soma dos seus coeficientes binomiais é igual a:
A) 64
B) 80
C) 128
D) 256
E) 512
Resolução:
Alternativa D
Sabemos que os coeficientes de um binômio de Newton (a + b)n serão iguais aos termos da linha n do triângulo de Pascal. Queremos então a soma de todos os termos da linha 8 do triângulo de Pascal, o que pode ser calculado por 28 = 256.
Questão 2
(Unifor) A soma da expressão a seguir é igual a:
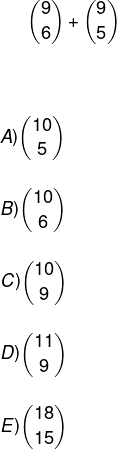
Resolução:
Alternativa B
Pela relação de Stifel, sabemos que:
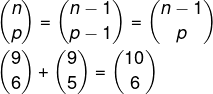
Artigos Relacionados

Últimas notícias
Outras matérias


















