Valor de pi
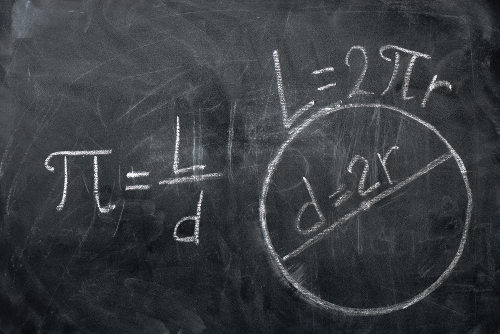
A legra grega π (pi) é usada para representar uma constante matemática considerada como uma das mais importantes já criadas. O valor de π é um número decimal não periódico com infinitas casas decimais, e é costume que vestibulares, Enem, concursos e todo tipo de questão envolvendo essa constante arredondem-na para 3,14.
Entretanto, pi é um número irracional. Isso significa que não pode ser expresso na forma de fração, é decimal e suas casas decimais são infinitas e (até onde são conhecidas) não seguem um padrão como o das dízimas periódicas.
Obtendo o valor de pi
Quando o comprimento da circunferência é dividido pela medida do seu diâmetro, o valor obtido sempre poderá ser arredondado para 3,14.
Uma das técnicas que podem ser usadas para encontrar uma aproximação mais precisa para o valor de pi foi desenvolvida por Arquimedes. O método usado por ele é chamado de exaustão e consiste em calcular uma aproximação do valor de pi por meio de polígonos com perímetros muito parecidos com o de uma circunferência.
Primeiramente, ele construiu um quadrado inscrito de perímetro “P” e outro circunscrito de perímetro “p”, ambos em uma circunferência de raio r. Sabendo que, ao dividir o perímetro C da circunferência por seu diâmetro 2r, obtemos o valor de pi, ele pôde construir a seguinte desigualdade:
p < C < P
2r 2r 2r
p < π < P
2r 2r
Dessa forma, pi é um número encontrado entre os perímetros do quadrado menor e do quadrado maior, ambos divididos pelo diâmetro.
.jpg)
Quadrado inscrito e quadrado circunscrito na circunferência
A grande ideia é aumentar o número de lados dos polígonos, de modo que eles sempre sejam regulares, fazendo com que seu formato se aproxime do formato da circunferência. Observe a seguir uma circunferência que inscreve e que circunscreve polígonos regulares com oito lados.
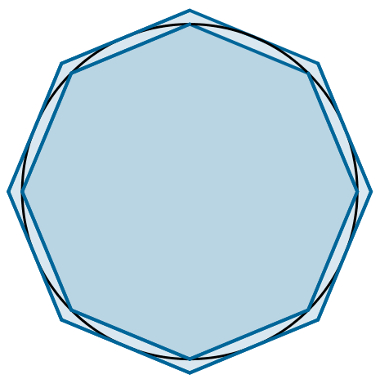
Octógono inscrito e octógono circunscrito na circunferência
Note que o perímetro dos polígonos se aproxima muito do perímetro da circunferência. Isso significa que, utilizando a mesma desigualdade anterior para os perímetros dessas figuras, obteremos uma aproximação muito melhor para o valor de pi.
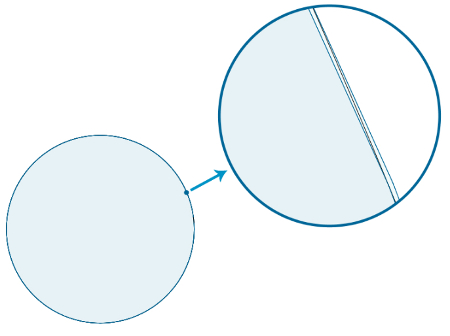
Arquimedes fez esses cálculos para polígonos com 96 lados. Veja na figura a seguir o quanto essa aproximação é precisa:
Essa imagem mostra que os dois polígonos têm o perímetro muito próximo à medida do comprimento da circunferência e, ao mesmo tempo, mostra por meio do zoom que um deles está inscrito e o outro circunscrito.
Na utilização da desigualdade anterior para aproximação de pi, nesse caso, as medidas dos perímetros encontrados para os polígonos foram:
p = 22
2r 7
e
P = 223
2r 71
Ou seja,
22 < π < 223
7 71
3,14285714 < π < 3,14084507
Aproximadamente.
Hoje conhecemos mais de 4 quatrilhões de casas decimais de pi, que foram calculadas por supercomputadores.
Artigos Relacionados

Últimas notícias
Outras matérias