Volume da esfera
Volume da esfera é calculado com base no raio (r), que, em suma, é o único elemento constituinte desse sólido. Existe mais de uma maneira de construir-se uma esfera. Nesse sentido podemos pensar, por exemplo, na sobreposição de circunferências, na qual os raios variam ou pela revolução de um semicírculo ou pelo conjunto de pontos do espaço, em que a distância desses pontos até o centro da esfera é sempre menor ou igual ao raio.
Leia também: Noções primitivas de geometria: ponto, reta, plano e espaço
O que é uma esfera?

Do estudo da circunferência sabemos que o diâmetro é o dobro do valor do raio. Assim, definimos uma esfera como sendo um sólido tridimensional restringido por uma superfície de rotação que possui todos os pontos equidistantes, ou seja: possui a mesma distância de um ponto do seu interior, ponto esse que chamamos de origem.
A superfície da esfera é obtida a partir da revolução (rotação) de uma semicircunferência em torno do diâmetro.
Leia também: Elementos do Círculo e da circunferência
Regiões da esfera
O ponto O é o centro da esfera e o segmento OB é chamado de raio da esfera.
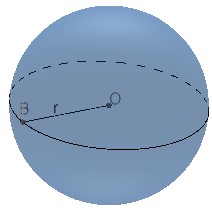
Podemos dizer que os pontos do espaço que estão a uma distância do centro O maior que o raio r compõem o exterior da esfera. Matematicamente estamos dizendo que o conjunto de pontos P vai estar fora da esfera se:
dOP > r
De maneira análoga, os pontos do espaço que estão a uma distância do centro O menor que o raio r compõem o interior da esfera. Ou seja, o conjunto de pontos P para estarem dentro da esfera devem satisfazer a condição:
dOP < r
Os pontos do espaço cuja distância até o ponto O é exatamente igual ao raio compõem a superfície ou a “casca” da esfera.
dOP = r
Como calcular o volume da esfera?
Considere uma esfera de raio r.
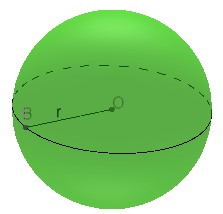
O volume da esfera é dado pela relação seguinte:
V = 4 · π · r³
3
Veja também: Diferenças entre figuras planas e espaciais
Exercícios resolvidos
Questão 1. Calcule o volume da esfera cuja medida do raio é de 10 cm.
Solução
Como o raio da esfera mede 10 centímetros, basta substituirmos essa medida por esse número na expressão:
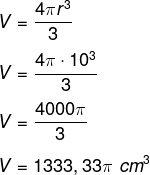
Questão 2. (Enem) O núcleo de uma bomba atômica tem o formato de uma esfera de raio r = 7,15 cm. Assim, o volume da esfera e a massa de urânio 235 que essa esfera comporta serão iguais aproximadamente a:
(Dados: π = 3,14 e densidade do U235 = 17 g/cm3)
a) 1530 cm3 e 26 kg
b) 1500 cm3 e 26 kg
c) 1530 cm2 e 24 kg
d) 1500 cm3 e 24 kg
e) 1530 cm3 e 24 kg
Solução
Sabemos que o volume da esfera é dado pela seguinte relação e substituindo o valor do raio que foi dado pelo enunciado temos:
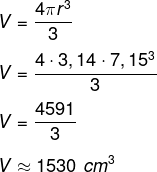
No enunciado temos que a cada centímetro cúbico temos 17 g de urânio. Como encontramos um volume de 1530 cm³ de urânio, teremos que:
m = 1530 · 17 = 26010g
m ≈ 26 kg
Alternativa a
Artigos Relacionados

Últimas notícias
Outras matérias


















