Constante de Avogadro

Conforme explicado no texto Mol, os cientistas procuravam por uma unidade que abrangesse um conjunto com um número imenso de moléculas, cuja massa pudesse ser medida. Foi aí que surgiu o conceito de mol. Dessa forma, 1 mol de qualquer substância apresenta uma quantidade de átomos que, se for “pesada” em gramas, terá o mesmo número da massa atômica.
Observe a reação a seguir de formação da água:
2 H2 + 1 O2 → 2 H2O
Os coeficientes dessa equação indicam que 2 mols de gás hidrogênio reagem com 1 mol de gás oxigênio para formar 2 mols de água. Sabemos que a massa atômica do hidrogênio é aproximadamente igual a 1,0 u ou 1,0 g, então 1 mol de H2 possui massa molecular igual a 2,0 g. Cada átomo de oxigênio possui massa atômica igual a 16 u, então a massa molecular de 1 mol de O2 é 32 g. Por fim, a massa molecular de 1 mol de água é 18 g (2,0 + 16,0).
Veja que esses valores seguem a Lei de Proust (Lei das Proporções Constantes), que diz que a proporção em massa das substâncias que participam de uma reação e que são produzidas é fixa, constante e não varia.
2 H2 + 1 O2 → 2 H2O
2 mol . 2,0 + 1 mol . 32 = 2 mol . 18
36 g = 36 g
Mas surgiu uma questão: Qual é a quantidade de partículas elementares (átomos, moléculas, íons, elétrons etc.) que compõem 1 mol?
O químico italiano Lorenzo Romano Amedeo Carlo Avogadro (1776- 1856) foi o primeiro cientista a ter a ideia de que uma amostra de um elemento, com massa em gramas numericamente igual à sua massa atômica, apresentaria sempre o mesmo número de átomos. Esse raciocínio também se aplica às moléculas ou fórmulas unitárias. Dessa forma, podemos concluir que 1 mol de hidrogênio, por exemplo, tem a mesma quantidade de átomos que 1 mol de oxigênio e que esse valor também é igual à quantidade de moléculas em 1 mol de água.
1 mol de H = 1,0 g = N átomos
1 mol de H2 = 2,0 g = N moléculas
1 mol de O = 16,0 g = N átomos
1 mol de O2 = 32,0 g = N moléculas
1 mol de H2O =18,0 g = N moléculas
O próprio Amedeo Avogadro não conseguiu determinar qual seria o valor de N. Mas com o passar do tempo e com o desenvolvimento da tecnologia, surgiram vários equipamentos e métodos que possibilitaram a determinação da quantidade de entidades contidas em 1 mol de qualquer substância.
Entre essas técnicas, a mais utilizada hoje é a difração de raios X, que consegue determinar o volume de alguns átomos em um retículo cristalino cuja massa de 1 mol de átomos e a densidade da amostra sejam desconhecidas. Assim, hoje sabemos que a constante de proporcionalidade que permite a passagem de quantidade de matéria para o número de partículas elementares é igual a: 6,022 . 1023.
Esse valor passou a ser chamado de constante de Avogadro ou número de Avogadro, em homenagem a Amedeo Avogadro.
Sabemos então que:
1 mol de H = 6,022 . 1023 átomos de hidrogênio
1 mol de H2 = 6,022 . 1023 moléculas de gás hidrogênio
1 mol de O = 6,022 . 1023 átomos de oxigênio
1 mol de O2 = 6,022 . 1023 moléculas de gás oxigênio
1 mol de H2O = 6,022 . 1023 moléculas de água
O Sistema Internacional de Unidades estabelece que, quando se trabalha com o mol, é necessário especificar qual é a entidade elementar. Observe isso no esquema a seguir:
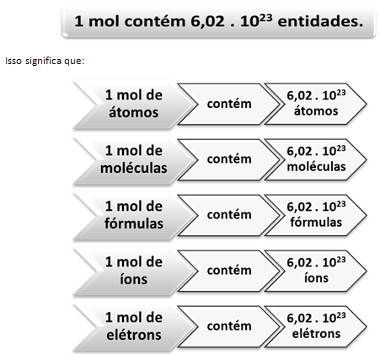
1 mol contém a constante de Avogadro
Esse raciocínio é o mesmo que se aplica, por exemplo, quando se diz “Quero uma dúzia!”, mas “uma dúzia de quê”? De bananas? De ovos? Do que, afinal? Assim como a palavra “dúzia” indica que são doze unidades, 1 mol indica que são 6,022 . 1023 unidades, mas é necessário especificar se é de moléculas, átomos, íons, etc.
Esse valor é extremamente grande. Para se ter uma ideia, para contar de 1 a 6,022 . 1023 na velocidade constante de 1 número por segundo, o tempo que levaria seria de 19. 098. 807. 000. 000. 000 de anos!
Artigos Relacionados

Últimas notícias
Outras matérias


















